
在实际工程中,我们经常会遇到很多随机振动的问题。许多随机过程都遵守着高斯分布规律,高sigma激励发生的概率很低,因此我们在实际计算中一般取3sigma为计算的上限。在随机振动控制系统的运行过程中,随机激励信号中产生的3sigma以上的峰值信号,可能会引起功放的输入过高而导致报警。所以我们在随机试验中,经常对驱动信号进行3sigma剪切,将3sigma以上的峰值信号剪掉,以保证功放在大量级随机振动试验时的电压输入不会因过高而报警,从而保证功放的输出功率。
今天我们以VENZO 880振动控制器的随机模块为基础,一起来了解sigma剪切,希望通过本文的介绍,能给大家在工作和学习中提供一些有意义的参考!
PART1 3 sigma原则
一般我们做的随机振动试验,如无特殊说明,都是按照高斯分布来实现随机化的。
高斯分布其实就是随机振动信号在幅值域呈现出的分布特性。标准的高斯分布,符合下图的描述:
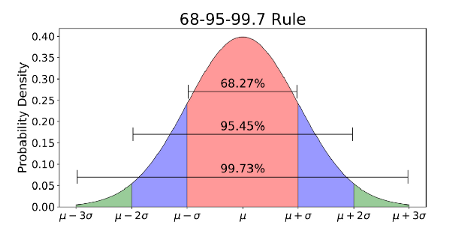
其中:σ是希腊字母,英文表达sigma,汉语译音为“西格玛”。在高斯分布中σ代表标准差,μ代表平均值。
高斯分布的随机信号存在3 sigma原则,3 sigma原则即为:
数值分布在(μ—σ,μ+σ)中的概率为68.27%;
数值分布在(μ—2σ,μ+2σ)中的概率为95.45%;
数值分布在(μ—3σ,μ+3σ)中的概率为99.73%;
在随机试验中,均值为0,标准差即是有效值,所以上述原则也可描述为:
68.27%的数值分布在1倍有效值以内;
95.45%的数值分布在2倍有效值以内;
99.73%的数值分布在3倍有效值以内;
也就是说数值超出3倍有效值的概率大约为0.3%,按正常随机信号的分布规律,每1000个点会有3个点超出3倍有效值的范围,按照采样率2560Hz来计算,则每秒会有7-8个点超出3倍有效值。
PART2 sigma剪切的应用
在航天航空、电子及电气元件等工程技术领域,大量的环境振动是随机振动。其中一部分随机试验因量级较大,常需要进行sigma剪切。 如GJB360B-2009电子及电气元件试验方法中,表214-1试验条件K中的加速度有效值为47.23g。
VENZO 880振动控制器的随机模块中运行两次该试验,依次为sigma 剪切禁用和迭代3sigma剪切。下图分别为在sigma 剪切禁用和迭代3sigma剪切时的时域记录信号。
sigma 剪切禁用:
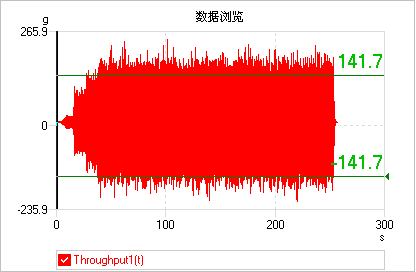
迭代3sigma剪切:
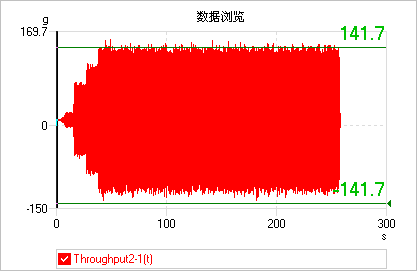
通过比较,我们发现,使用了迭代3sigma剪切的时域信号,其峰值信号超出±3sigma的概率明显降低。
PART3 sigma剪切的特点
VENZO 880振动控制器软件中,包含两种sigma剪切选项:“常规”和“迭代”。“常规”选项跟市场上大多数控制器剪切方法一样,直接对驱动电压信号进行数字式剪切,这种方法的优点是简单,运算量小,缺点是波形失真度大,控制谱的动态范围明显降低,响应信号的峰值因子减小不明显。
为了更好地满足用户的需求,我们振动控制器软件中的sigma剪切增加了“迭代”选项。“迭代”法基于时域裁剪和频域相位调整算法,使得迭代sigma剪切相对于常规sigma剪切,拥有两大优点:剪切效果更好,控制动态范围更大。
剪切效果更好
VENZO 880振动控制器的随机模块中,通过迭代sigma剪切,可使得有效值较大的随机试验在运行过程中,保证没有过大的驱动峰值信号进入振动台系统。
如GJB360B-2009中表214-2试验条件K中的加速度有效值为54.855g,如下图所示。
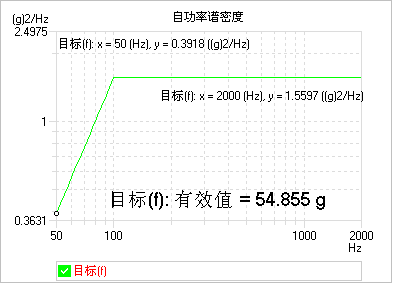
使用迭代3sigma剪切,加速度时域记录信号如下图所示。可以看出,时域的峰值为180.98g,大约为有效值的3.3倍。
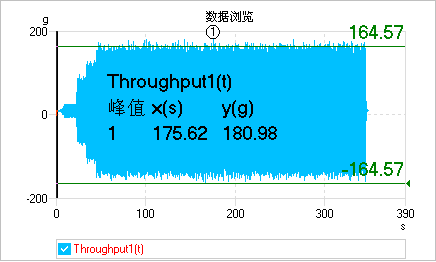
如果使用市场上流行的常规3sigma剪切,加速度时域记录信号如下图所示。可以看出,时域的峰值为224.97g,大约为有效值的4.1倍。
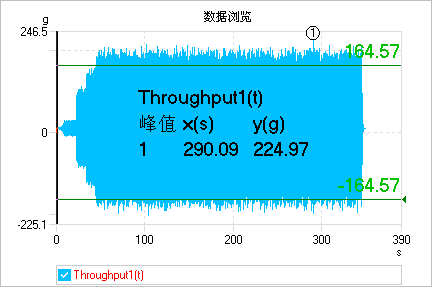
可以看出,迭代sigma剪切的剪切效果更好,能更好地保证试验的安全性和可靠性。
控制动态范围更大
VENZO 880振动控制器随机模块中,使用迭代法sigma剪切,能够保证在sigma剪切系数大于2.8时,控制谱的动态范围不受丝毫影响。
下图为使用迭代3sigma剪切,90dB随机谱图的控制效果,控制的动态范围可达90dB。
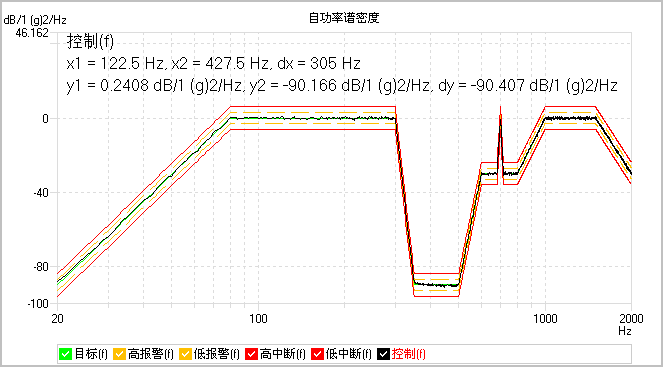
下图为采用市场上流行的常规3sigma剪切,90dB随机谱图的控制效果,控制的动态范围大约为40dB。
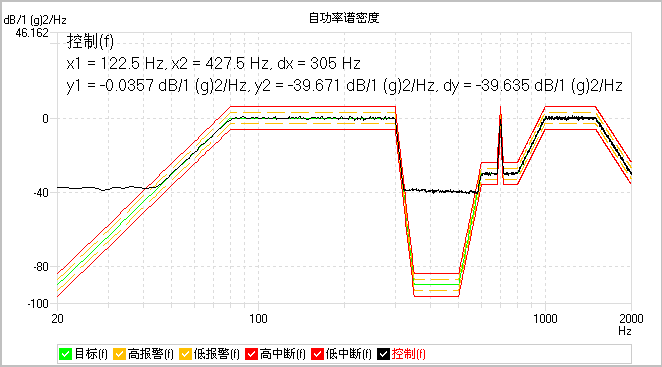
可以看出,迭代sigma剪切的控制动态范围更高,能更好地满足动态范围大的随机试验进行sigma剪切的需求。